Electricity is generated by generating stations and transmitted to load centers from where it is distributed to end consumers. These load centers are controlled by distribution utilities, and there is an inter-change of energy between different utilities connected to the grid.
Consumers connected to the distribution utilities, though consuming active energy may or may not consume reactive energy. There may be consumers whose loads are predominantly inductive and other consumers whose loads are predominantly capacitive. There may be bulk consumers who have their own generators who operate their generators in synchronism with the grid, drawing active energy from the system or even exporting active energy into the system.
The exchange of electricity is complex in such situations, and four quadrant energy measurements are needed to accurately measure the active and reactive energy under different export/import conditions for both active & reactive energy.
Energy measurement under such situations will depend on applicable tariff structures, and hence to cater for different tariff structures in the environment of import/export of active/reactive energy special data logging/measuring features are required in meters. In this regards there are three forms of measurements to deal with (in metering) and these are active energy, reactive energy & apparent energy. The definitions and inter-relations are explained for import/export are explained below.
We need to understand the definition of power flow. Power flow is always measured with respect to the Voltage, and the Voltage at the point of measurement is taken as reference vector for defining the direction of power flow. The angular position of the current vector with reference to this reference Voltage vector defines the direction of the flow for active, reactive and apparent energy.
When we consider vectors, and we assume that the voltage vector is a reference vector (with the current vector as a variable vector based on the load), the
current vector may assume any position within 3600 of the voltage vector. Suppose we now divide the 3600 into four equal quadrants of 900 each, we shall have four quadrants, and for import/export of active/reactive power, the current vector can lie in any of the four quadrants. Let us call these quadrants as Quadrant 1, 2, 3 & 4.
When the current vector is placed in any of these quadrants, it forms an angle with respect to the voltage vector. The in-phase component of the current, arrived at by considering the Cosine of the angle between the voltage & current vectors is known as the active current. Multiplication of this active component of the current with the voltage gives us the active power. The integration of the active power with time gives us the active energy.
The quadrature component of the current, arrived at by considering the Sine of the angle between the voltage & current vectors is known as the reactive current. Multiplication of this reactive component of the current with the voltage gives us the reactive power. The integration of the reactive power with time gives us the reactive energy.
The point to emphasize is that the reference point or point of measurement is critical in defining whether the power (both active or reactive) is “imported” or “exported”, and it is with respect to the Voltage vector at this reference point that the definitions are made.
The diagram shown below illustrates two positions of measurement and defines the import and export of electricity in accordance to the above definition.

Shown in the above example is a condition where power (in general) is flowing from utility A to B.
At point “A” the power is being exported and at point “B” the power is being imported. These import/export definitions are always with respect to the voltage vectors at the respective points. Hence, to be able to measure the import & export correctly, we have to see these with relation to the polarity of current connections of the meter. Incorrect current connections at the meter end will result in an “export energy” to be recorded as an “import energy” and vice versa. There is therefore a need to check connections of meters carefully in the field.
It is now explained how the angle of 3600 can be divided into 4 quadrants of 900 each. The active/reactive power flow is defined as per these 4 quadrants by IEC 62053-23, with the voltage at the measuring point taken as the reference vector at vertical position shown as the 00 position.
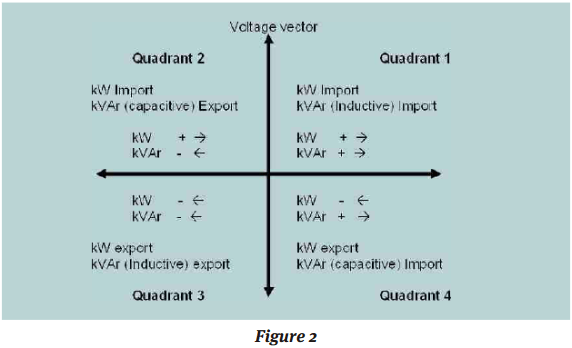
The 4 quadrants are illustrated in Figure 2 below. Illustrated in the diagram are the vectorial position of the current with respect to the voltage to show what is meant by import and export for active and reactive power (or energy).
The power flow quadrants as per IEC 62053-23 are shown in the figure 3.
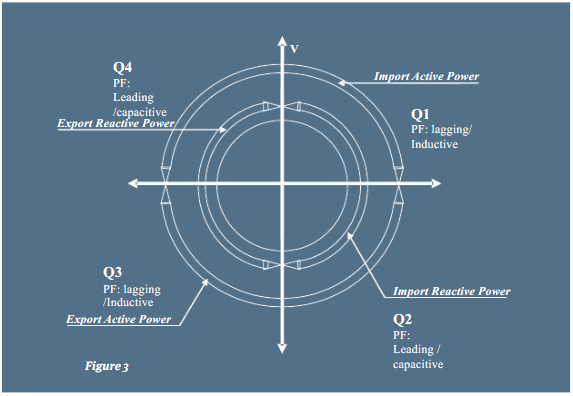
The loads are comprised of a combination of inductive load, resistive load, and capacitive load. The current vector can be a maximum 90 away from the voltage vector when the load is either inductive or capacitive. It is in-phase with voltage when the load is resistive.
When the angle between the voltage and active component of current is 00 degrees, the power flow is considered as “ active import”. All energy recorded by the energy meter for this type of power flow is recorded as “import energy”.The current vector lies in either quadrant 1 or 2, active energy is being consumed. The quadrants defined in IEC for active energy import are 1 & 4 as shown in figure 3.
When the angle between the voltage and active component of current is 1800 degrees, the power flow is considered as “active export”. All energy recorded by the energy meter for this type of power flow is recorded as “active export energy”. The current vector lies in either quadrant 3 or 4 active energy is being generated. The quadrants defined in IEC for active energy export are 2&3 as shown in figure 3
There can be two types of reactive power (or energy), namely (i) capacitive power and (ii) inductive power.
When the angle between the voltage and reactive component of current is 900 degrees, the power flow is considered as “ reactive import”. All energy recorded by the energy meter for this type of power flow is recorded as “import of reactive energy”. When the load (or power) is capacitive, the current vector leads the voltage vector. The current vector therefore lies in Quadrant 2 (or 3) depending on whether the capacitive load is import or export, and the quadrature component of the load current (capacitive current) is either at a 900 angle or 2700 with respect to the voltage vector, as shown in figure 2. This reactive energy is called Reactive energy capacitive or simply Reactive energy lead.
When the angle between the voltage and reactive component of current is 2700 degrees, the power flow is considered as “reactive export”. All energy recorded by the energy meter for this type of power flow is recorded as “active export energy”. When the load (or power) is inductive, the current vector is leads the voltage vector. The current vector lies in Quadrant 1 (or 4) depending on whether the inductive load is import or export, and the quadrature component of the load current (reactive current) is either at 2700 angle or 900 angle with respect to the voltage vector as shown in figure2. This reactive energy is called Reactive energy Inductive energy or simply Reactive energy lag.
Reactive energy is always defined in association with active energy. Thus reactive energy is defined for each quadrant separately. Based on the quadrant, reactive energy is either an import reactive energy or an export reactive energy. The form of reactive energies are defined as: Reference Figure 2.
Apparent energy is essential the product of the scalar values of the voltage and current. Because the current vectors can lie in any of the four quadrants, it is not sufficient to define the apparent energy as the product of voltage and current. For every type of energy we need to define a direction to state whether the energy is being imported or exported, and the same is also needed for apparent energy. Hence defining apparent energy is not as simple as stating that it is the product of voltage & current.
Apparent energy is the product of voltage & current (scalar quantities) and is considered as “apparent import” in case the current vector lies in Quadrant 1 or 2, and “apparent export” in case the current vector lies in Quadrant 3 or 4.
The quantities measured by meters are the active and reactive components of the current (with angle). Hence, using these values the apparent energy can be defined in two different ways, and it is important to recognize that for each of these definitions we shall get a different value for the apparent power (or energy).
In the first definition, the apparent power can either be defined as the Pythagoras Sum of “sum of inductive plus capacitive” and the “corresponding active power” .
In the second definition, the apparent can be defined as the Pythagoras Sum of “sum of inductive component only” and the “corresponding active power”.
As both the definitions do not give the same “value” for apparent power, the concept of having apparent energy tariffs can be fraught with misunderstanding. (There are of course many other technical & commercial reasons why tariffs based on apparent energy is illogical)
The Apparent power is called as “import apparent power” when current vector lies in quadrants 1 or 2 as shown in figure 1. Apparent power in quadrant 3 and 4 is called as “export apparent power”, in these quadrants active power is exported
As we have seen, different energies can be defined as “Active”, “Reactive” and “Apparent” based on the direction of active energy and in relation to the position of the voltage vector at the point of measurement. The following energy registers are required to record them accordingly
(i) Active import
(ii) Active export
(iii) Reactive (inductive) while active import
(iv) Reactive (capacitive) while active import
(v) Reactive (inductive) while active export
(vi) Reactive (capacitive) while active export
(vii) Apparent import (based on definition of apparent energy)
(viii) Apparent export (based on definition of apparent energy)
An example of a single tie line with generators and loads are shown in the fig 2.
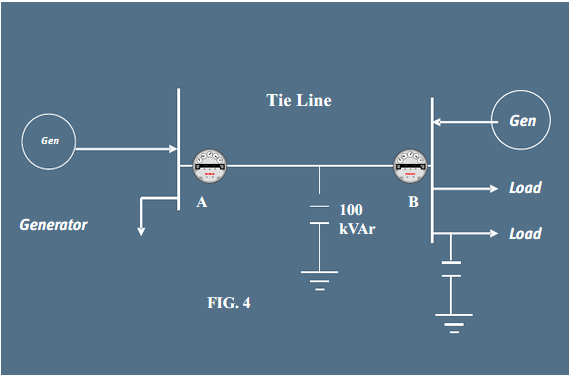
As shown above, various loads are connected to the system. These loads can be inductive, capacitive, resistive, or mixed. Generally, the loads are mixed with some active & some reactive component, but in the reactive component, they may be either predominantly inductive or predominantly capacitive.
The lines (shown above as a tie-line) are generally long HT lines that have a significant capacitance. The tie line capacitance for the above example is assumed as 100 kVAr. The points marked as “X” are the locations where meters are installed.
Let’s consider point B as a metering point and examine the different load conditions. As meters are installed, the increment of the energy registers will depend on the vectorial position of currents at the metering point with respect to their respective voltages.
Case 1 – the load at metering point “B” is predominantly inductive but more than the VARs generated by the tie-line.
When the load is inductive, it draws reactive power from the system (i.e. grid). This reactive power requirement is met by capacitances in the system (synchronous condensers, fixed/switched capacitors, generators supplying
VARs, the capacitance of the lines, etc.).
If the reactive requirement of the inductive load is more than the reactive VARs generated by the tie-line capacitance, the generator will start supplying reactive energy to meet the reactive demand of the load. Under these conditions the load and meter (at point B) will operate in quadrant 1 but the generator (and the meter at point A in generator end) will operate in quadrant 3.
Suppose the capacitance of the tie-line (i.e. the 100 kVAr generated by the tie-line) meets the reactive requirements of the load reactive power will flow from the tie line to the load to meet the reactive demand and this will be measured by the meter located at point “B”. It may be noted that there will be no reactive flow towards the metering point located at “A”.
At Point B, active & reactive power is sensed as being “imported” and the current vector will lie in Quadrant 2.
Case 2 – The load at metering point “B” is predominantly capacitive
If the reactive requirement of the load is capacitive, the reactive VARs generated by the tie-line and the capacitive reactive energy of the load will flow towards the generator side. The meter connected at the generator end will operate in quadrant 4 and the meter at metering point B will operate in quadrant 2.
When the load is predominantly capacitive, reactive energy will flow from the load into the system (grid). The tie line capacitance and load capacitance will add up and flow towards the generator and become a reactive energy reserve for the grid. This will lead to two conditions
Under these conditions, at point B reactive power will flow from the tie line, and sum of both load-end reactive power and tie line’s reactive power will flow towards the meter located at point A near the generator. The point B (load end meter) will operate in Quadrant 2, and the point A meter will operate in Quadrant 4.
The different conditions can be explained in the way stated above for other quadrants as well, by assuming that the tie-line is predominantly inductive instead of capacitive.