Synopsis
The issue of harmonics is debated at various levels. Harmonics are generated in the system. Generally the effect of harmonics is studied in voltage or current. The current harmonics flow in the system generates voltage harmonics which results into power harmonics. Power harmonics are than measured by energy meters. The flow of power harmonics and it effect on the energy measurement is discussed in this paper. Though current harmonics are high, power harmonics are very small and contribution to energy is insignificant. The power harmonics direction is opposite to fundamental power flow at the source of harmonics so total power measured is less than fundamental power. The linear loads consumes harmonics power from the system.
alternating current electrical power, thus a utility delivers sinusoidal power or fundamental power to consumers. The loads at consumer end are nonlinear in nature and cause distortion in the wave shape and generate other components at frequencies that are integral multiples of the fundamental frequency. The combined wave shape of all the frequencies is not a sinusoidal wave shape and make an irregular shape but of repetitive nature. The repetitive deviation of either the voltage or current waveform from a pure sinusoid is usually referred as harmonic distortion. The combined wave shape is a complex wave shape and can be decomposed by Fourier transform method.
The distortion components can be submultiples of the fundamental frequencies in a power system and cause distortion in the sinusoidal wave shape and are called harmonic distortion but generally the integer multiples are referred as harmonic components and are harmonic distortion. The harmonic components may be different in current and voltage waveforms
Harmonics are generated by any load, which draws current not proportional to the voltage applied. Most loads are somewhat nonlinear, but some generate more and higher level harmonics than others. These include the following and many more types of loads
The sinusoidal voltages or fundamental value of voltage is defined by the equation
‘ E=Em Sin wt
‘ I=Im Sin wt
Em and Im are the peak values. The RMS values and peak values has a ratio of 0.707.
Let the complex voltage waveform be represented by the equation
‘E = E1m Sin wt+E2m Sin 2wt + E3m Sin 3wt + E4m Sin 4wt +…+ Enm Sin nwt
is applied to a circuit. Let the equation of the resultant current wave be
‘I= I1m Sin (wt+1) +E2m Sin (2wt+2) + E3m Sin (3wt+3) + E4m Sin (4wt+4)
+…+ Enm Sin(nwt+n)
The instantaneous value of the power in the circuit is p=ei watt For obtaining the values of this product, we will multiply every term of the voltage wave, in turn, by every term in the current wave. The average power supplied during a cycle would be equal to the sum of the average values over one cycle of each individual product term. Hence total power supplied by a complex wave is the sum of the average power supplied by each harmonic component acting independently.
Total power is P= E1I1cos1 + E2I2 Cos 2 + E3I3 Cos 3 + ……EnIn Cosn
The first component is the fundamental power and other components are harmonic components. Hence the total power is a sum of fundamental power and harmonic power. The direction of flow of individual component should be considered appropriately.
A complex waveform consisting offundamental and third harmonics is shown in the figure below.
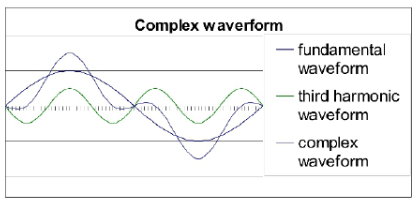
In three-phase system, harmonics may be produced in the same way as in the single-phase systems. In the three phase systems following need to be considered
The Diagram of metering point and load is shown below
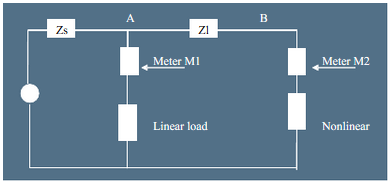
The simple and common power system connections can be used to understand the flow of harmonic power in the system due to nonlinear loads.
Vg is the generator of the utility, which generates fundamental power. The Zs is the source impedance and Zl is the distribution network impedance, which a load see from the load end. The Zl causes drop in the voltage due to load current. Meter M2 measures power drawn by the nonlinear load. The voltage distortion at the point marked A and B depends on the impedances Zs and Zl. The linear load is connected in the system and power drawn by the linear load is measured by meter M1.
The fundamental power is generated by the generator and transmitted to the load via Zs and Zl. the harmonic current causes distortion in the voltage at the points A and B. The distortion in the voltage will depend on the impedances. And the magnitude of harmonics currents.
The nonlinear load draws a current with a complex waveform. The complex current wave shape will cause drop across the Zl and Zs. Consider the Zs and Zl as linear impedances, the drop will be same as complex current wave shape. The voltage at point B is Vg minus the complex voltage drop across the two impedances. Thus the harmonic power has negative sign as compared to the fundamental power.
The total power is the sum of fundamental power and harmonic power thus the total power measured by the meter M2 is fundamental power consumed minus the harmonic power generated. The harmonic power is flowing from the load to the utility and meters will measure less total power.
The complex current waveform will distort the voltage at the point A but the magnitude of distortion will be less as compared to the point B. The linear load will draw current proportional to the voltage. Thus it will draw some complex current due to the drop in the voltage due to complex current waveform. The complex current is in phase with the voltage applied thus the total power measured by the meter M1 is the fundamental power consumed by the load plus complex or harmonic power fed due to voltage at the point B. Thus the harmonic energy is flowing from the utility to the consumer and the power metered is more than the power actually consumed in the load.
Lets consider a simple mathematics to illustrate the above. 50% third harmonic current is generated by a load causes 10% drop in the voltage. The harmonic power is 10*50/100=5%. Thus Total power will be 95% of the fundamental power actually consumed in the nonlinear load. Thus a Total power meter will measure 5% less than a Fundamental power meter. The 10% drop will cause 10% harmonic current to flow in the linear load thus total power is 10*10/100=1%. Thus a total power will measure 1% more power than a fundamental power meter.
Some experiments have been conducted to prove the explanation and the results is shown in the table below
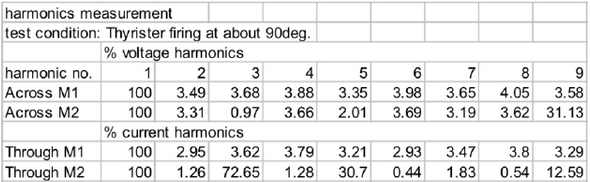
The fundamental values are considered as 100% and other harmonic components are presented corresponding to fundamental values.
The table below shows flow of harmonics corresponding to harmonics in voltage and current harmonics above.
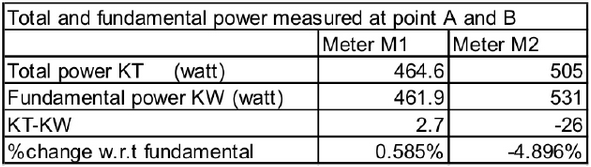
these results are taken by simulating the loads and high line impedances to enlarge the effect of harmonics.
The harmonics appear differently in the way the connections are done. 3phase 4 wire connected meter will measure the voltages phase to neutral and 3p3w meter measure the phase voltages thus both the meter will perceive different harmonics under the same harmonics flow in the system. The harmonics measurement is different in different type of connection as illustrated above in three phase systems. Thus the total power measured will also be different for the same harmonics in the system
Conclusion
It is evident from the test results and study done by various engineers across the world that the harmonics are generated by non-linear loads. The generated harmonics flow back to the system and cause heating in the lines, transformers, and capacitors. The resonance due to harmonics is quite common which leads to excessive RMS current and more loading than actual useful power transferred or delivered.
The total power measurement is always less than the fundamental power measurement. The consumer generating harmonics is metered less if total power is metered and consumers who are not generating the harmonics are absorbing harmonics and metered more than what is consumed. Total power and energy measurement system rewards consumers generating harmonics and polluting the electrical system and penalizes innocent and fair consumers.
The non-linear consumers are increasing and are more than linear consumers. The loss of revenue is much more due to harmonics generation than the gain in revenue due to harmonics power consumed when the total power is measured